 |
Für die Darstellung und Untersuchung funktionaler Zusammenhänge lassen sich Beispiele aus der Praxis verwenden. Das auf dem Raspberry-Pi basierenden digitale Messwerterfassungssystem DMSRP bietet eine sehr gute Anbindung des Mathematikunterrichtes an die Realität. Schüler*innen und Lehrkräfte können die kurze Anleitung zu experimenteller Aufzeichnung, Visualisierung und Auswertung der Messdaten direkt beim Experimentieren mit dem DMSRP und verschiedenen Sensoren verwenden. Hinweis: Bei Einführungen in Mathematikunterricht können Lehrkräfte die in .csv-Dateien gespeicherten Messdaten in eigen erstellten Aufgaben, Fragestellungen und Anwendungen verwenden. Mithilfe von Tabellenkalkulationsprogrammen lassen sich Eigenschaften von Funktionen untersuchen, sowie numerisches Differenzieren oder Integrieren durchführen. |
|
Lineare Funktionen |
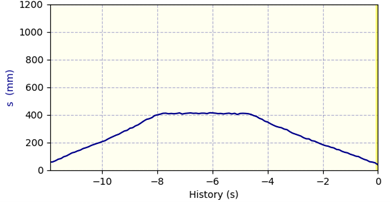
Zeit-Weg-Gesetz im DMSRP-Fenster
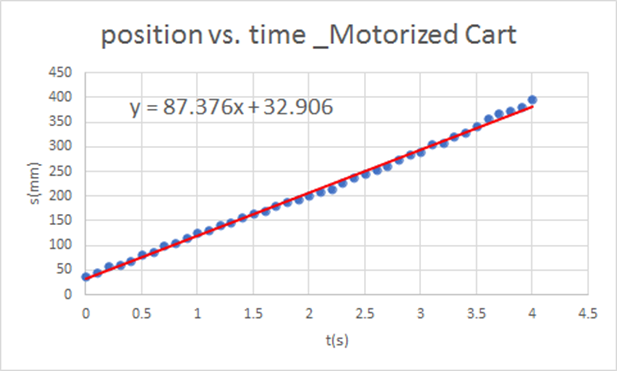
Regressionsgerade der Zeit-Weg-Messdaten |
Anleitung zum Aufbau und Durchführung des Versuchs findet man hier...
Gespeicherete Messdaten in .csv-Format findet man hier..s(t)_uniform_motion.csv
|
|
Quadratische Funktionen |
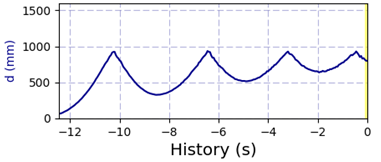
Zeit-Weg-Gesetz im DMSRP-Fenster
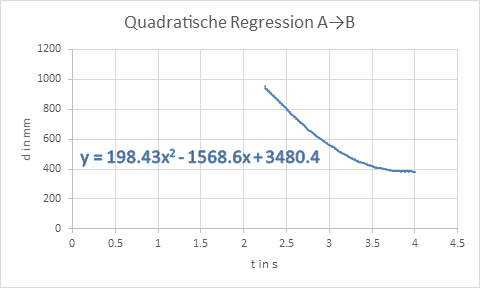
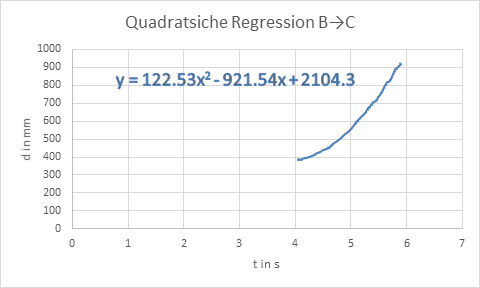
Regressionsgerade der Zeit-Weg-Messdaten (verzögerte Bewegung aufwärts)
Regressionsgerade der Zeit-Weg-Messdaten (beschleunigte Bewegung abwärts) |
Anleitung zum Aufbau und Durchführung des Versuchs findet man hier...
Gespeicherete Messdaten in .csv-Format findet man hier. s(t).csv
|
|
Trigonometrische Funktionen |
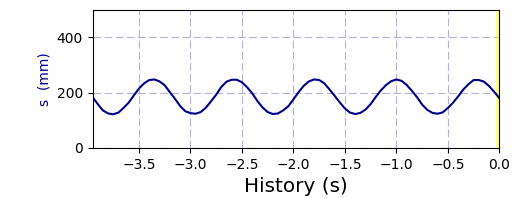
Zeitlicher Verlauf der Elongation eines Federpendels im DMSRP-Fenster
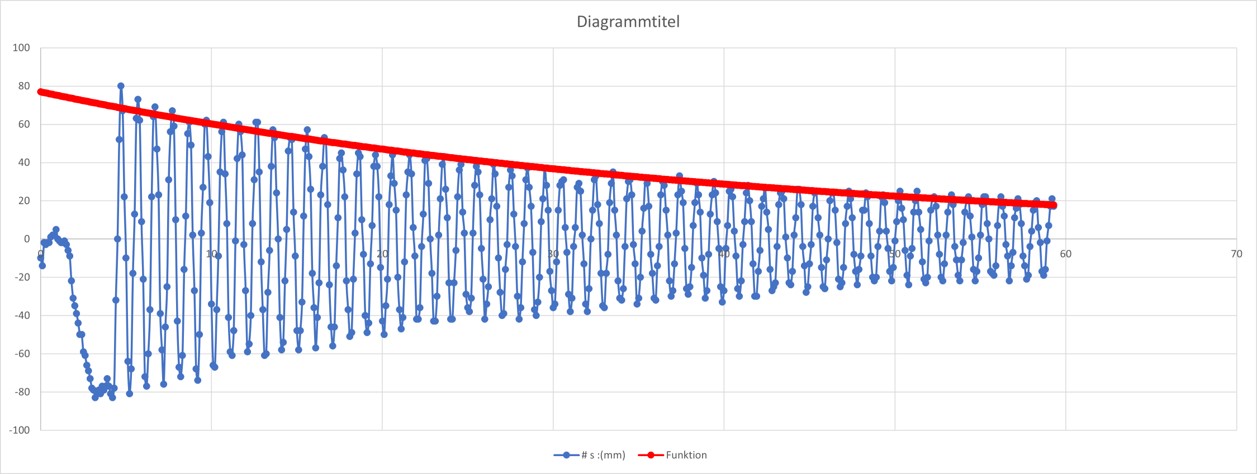
Grafische Darstellung der in .csv gespeicherten Messdaten einer gedämpften Schwingung
|
Anleitung zum Aufbau und Durchführung des Versuchs findet man hier...
Gespeicherete Messdaten in .csv-Format findet man hier: (s)t_Spring_Mass_Oscillator.csv
Numerische Lösung der Differentialgleichung eines Federpendels (ohne und mit Dämpfung) in JupyterLab im myBinder-Umgebung findet man hier
|
|
Exponentialfunktionen |
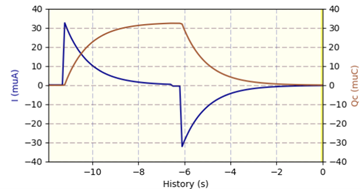
Zeitlicher Verlauf der Ladung am Kondesator und der Stromstärke durch den Widerstand im RC-Kreis visualisiert im DMSRP-Fenster
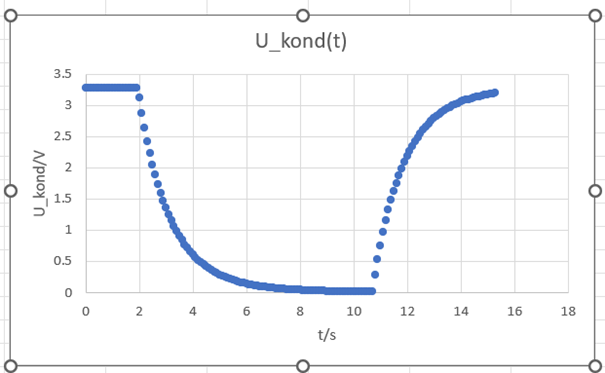
Grafische Darstellung der in .csv gespeicherten Messdaten für die Spanung am Kondensator
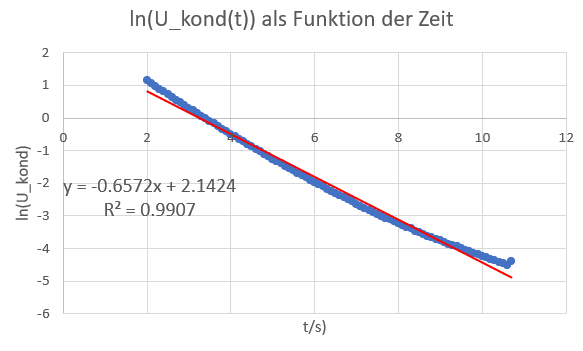
Linearisierung der Messdaten durch Logarithmieren der Spannung am Kondensator. Die Steigung der Regressionsgerade gibt den Kehrwert der Zeitkonstante an.
|
Anleitung zum Aufbau und Durchführung des Versuchs findet man hier...
Gespeicherete Messdaten in .csv-Format findet man hier: testfile_Uc(t)_C=10microF.csv
Aufgabenblatt findet man hier...
in JupyterLab findet man eine Anwendung zu den aufgezeichneten DMSRP-Messdaten des zeitlichen Verlaufs der Spannung am Kondensator. Diese werden mit Pandas ausgelesen und mit Matplotlib grafisch dargestellt. Weitere Untersuchungen wurden mit einem Python-Code erarbeitet. Die JupyterLab-Anwendung im myBinder-Umgebung findet man hier
|
|
Exponentialfunktionen mit Stätigungsgrenze |
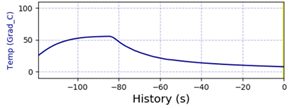
Zeitlicher Verlauf der Temperatur einer Flüssigkeit beim Aufwärmen und Abkühlen visualisiert im DMSRP-Fenster
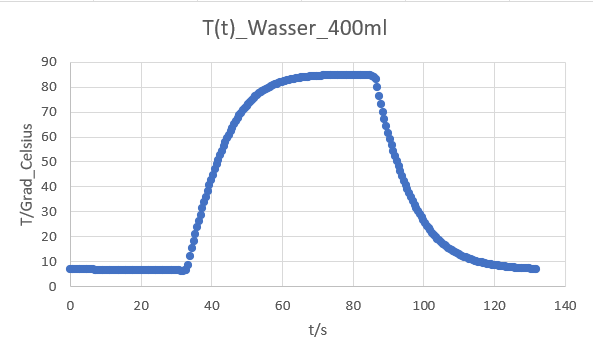
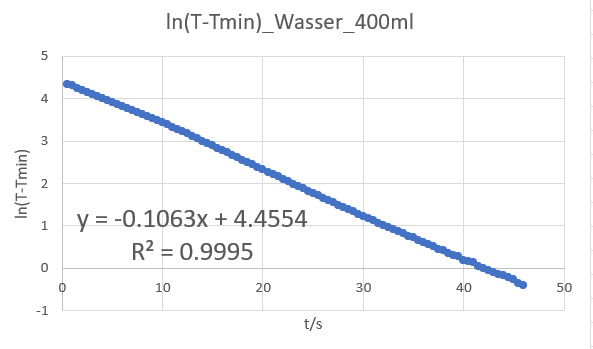
Grafische Darstellung der in .csv gespeicherten Messdaten für die Temperaturänderung mit der Zeit
Linearisierung der Messdaten durch Logarithmieren der Temperatur beim Abkühlen. Die Steigung der Regressionsgerade gibt den Kehrwert der Abkühlungskonstante an.
|
Anleitung zum Aufbau und Durchführung des Versuchs findet man hier...
Gespeicherete Messdaten in .csv-Format findet man hier
Ein Video zum Experiment findet man hier
in JupyterLab findet man eine Anwendung zu den aufgezeichneten DMSRP-Messdaten des zeitlichen Verlaufs der Temperatur. Diese werden mit Pandas ausgelesen und mit Matplotlib grafisch dargestellt. Weitere Untersuchungen wurden mit einem Python-Code erarbeitet. Die JupyterLab-Anwendung im myBinder-Umgebung findet man hier
|
|
Exponentialfunktionen mit positiver Wachstumskonstante |
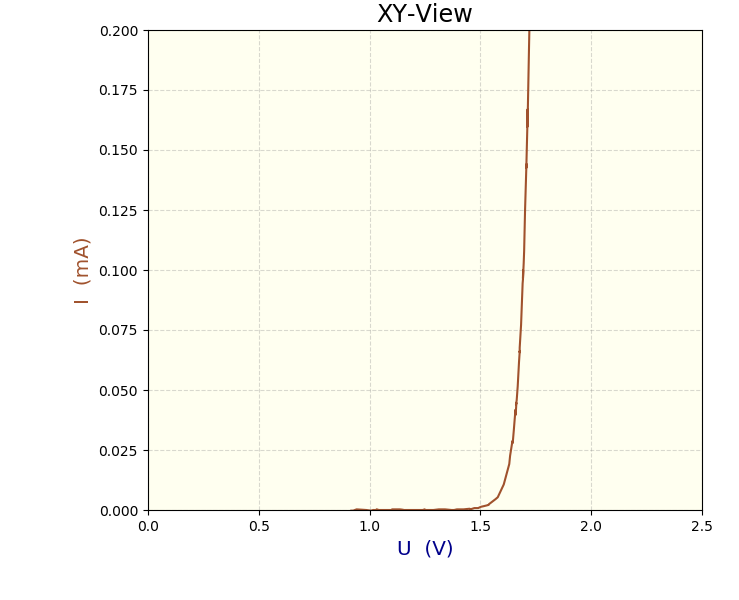
Kennlinie I(U) einer roten LED visualisiert im DMSRP-Fenster.
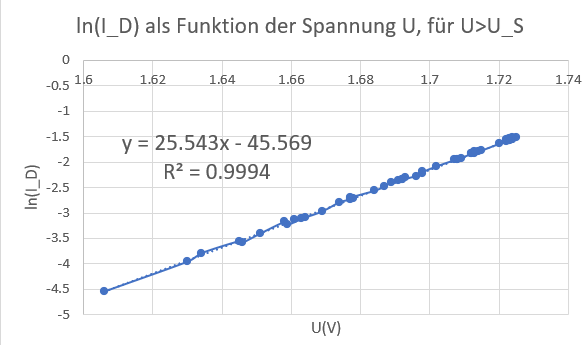
Grafische Darstellung der logarithmierten Stromstärkewerte in Anhängigkeit von Spannung U, für U > U_S im Durchlassbereich. Die U- und I-Werte findet man in .csv gespeicherten Messdaten. Die lineare Zunahme von ln(I_D) mit U bestätigt eine exponentiellen Zusammenhang mit positiver Wachstumskonstante gemäß der Shockley-Gleichung. |
Anleitung zum Aufbau und Durchführung des Versuchs findet man hier...
Gespeicherete Messdaten in .csv-Format findet man hier
Ein Video zum Experiment findet man hier
|
|
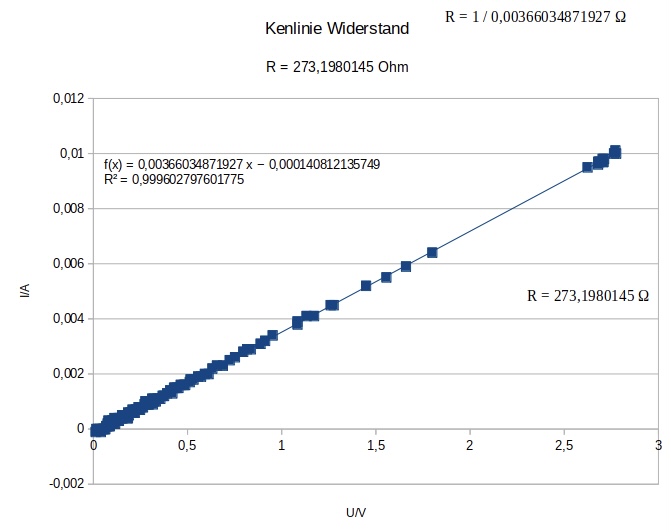
Proportionalität und lineare Funktione |
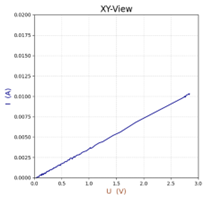
Kennlinie I(U) eines Widerstandes visualisiert im DMSRP-Fenster.
Grafische Darstellung der Stromstärke I in Abhängigkeit von der Spannun U. Die U- und I-Werte findet man in .csv gespeicherten Messdaten. |
Anleitung zum Aufbau und Durchführung des Versuchs findet man hier...
Gespeicherete Messdaten in .csv-Format findet man hier
|