 |
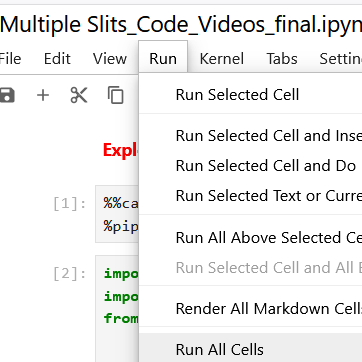
Neu: Einbettung des auf dem Raspberry Pi basierten Messwerterfassungssystems DMSRP in JupyterLab Notebooks Hinweis: Die Jupyter Notebooks kann man in mybinder Drucken Sie auf den Link und warten bis sich die JupyterLab Umbegung in MyBinder-Plattform öffnet. Danach drucken Sie auf Run und dann auf Run All Cells um die Interaktivität mit Sliders in der ausführbaren Umgebung von JupyterLab zu betätigen. Warten Sie bis alle Komponenten der JupyterLab Anwendung in MyBinder sichtbar und aktiv sind (es dauert ein Paar Sekunden). Sie können weiter in der JupyterLab Umbegung arbeiten, z.B. neue Python-Codes, Bilder, Videos und Texts ergänzen. Danach speichern Sie Ihre erarbeitete JupyterLab-Anwendung unter Ihren Namen und laden Sie diese auf Ihren PC (oder GitHub) herunter.
|
 |
Grundlage des auf dem Raspberry Pi basierten digitalen Messwerterfassungssystems DMSRP:
https://colab.research.google.com/drive/1NiuCeCgLjQF_YOWxen67WJdxmsv-W-2s?usp=sharing |
 |
Auflade- und Entladevorgang eines elektrolytischen Kondensators durch einen ohmschen Widerstand. Aufzeichnung mit dem Analog-Digitalwandler ADS1115 und Messwerterfassungssystem DMSRP in JupyterLab Notebooks
https://colab.research.google.com/drive/1I6uQ4Gcycz9u3CmW4eBkRMnStLcccMiY?usp=sharing
|
 |
Auswertung des mit dem DMSRP und ADS1115 Analog-Digital-Wandler aufgezeichneten Auflade- und Entladevorgangs eines elektrolytischen Kondensators. Die aufgezeichneten DMSRP-Messdaten des zeitlichen Verlaufs der Spannung am Kondensator werden mit Pandas ausgelesen und mit Matplotlib grafisch dargestellt. Aus den echten Daten werden einen Teil zum Entladen des Kondensators ausgewählt und logarithmisch linearisiert. Eine Regressionsgerade wird zu den logarithmierten Werten ln(U_C) mit einem Python-Code erstellet. Aus der Steigung der Geraden lässt sich die Zeitkonstante des RC-Schaltkreises ermitteln und weiter mit dem Wert aus R und C vergleichen.
|
 |
Auswertung des mit dem DMSRP und Widerstandstemperaturdetektoren PT100-RTD mit Verstärker - MAX31865 aufgezeichneten Aufwärmen- und Abkühlenvorgangs einer Flüssigkeit (200ml Spiritus). Die aufgezeichneten DMSRP-Messdaten des zeitlichen Verlaufs der Temperatur der Flüssigkeit werden mit Pandas ausgelesen und mit Matplotlib grafisch dargestellt. Aus den echten Daten werden einen Teil zum Abküklenvorgang ausgewählt und logarithmisch linearisiert. Eine Regrressionsgerade wird zu den logarithmierten Werten ln(T) mit einem Python-Code erstellet. Aus der Steigung der Geraden lässt sich die Wärmeübergangskonstante ermitteln.
|
 |
Low-Cost Licht-Scanner mit einer BPW34 Fotodiode mit einer sehr hohe Geschwindigkeit von 25ns und eine hochempfindliche Lichtfläche angeshlossen an einem Analog-Digital-Wandler ADS1115. Das Ziel ist es, die Aufzeichnung der Verteilung der Lichtintensität beim Einzelspaltversuch
https://colab.research.google.com/drive/1alg1QaYBJECo-M2Th8BUxUzQmprFmL6V?usp=sharing |
 |
Auswertung und mathematische Modellierung der DMSRP-Messdaten zur Beugung am Einzelspalt Hier findet man die in .csv gespeicherte Messdaten, ihre grafische Darstellung, Herleitung der Funktion für die Intensitätskurve der Beugungsfigur, eine dynamische GeoGebra-Simulation zum Zeigermodell und einen Python-Code mit Interaktivität zur Untersuchung der Beugungsfigur für unterschiedleichen Wellenlängen und Spaltenbreite.
Link zur vollständigen Untersuchung der Beugung am Einzelspalt
|
 |
Mathematische Modellierung und experimentelle Untersuchung der Interferenz am Mehrfachspalt. Hier haben Sie Interaktivität mit Sliders.
|
 |
Darstellung der Scahltung zur Untersuchung der Kennlinien einer Si-BPW34 Fotodiode. Der zeitliche Verlauf der Spannung, des Stroms und der Leistung der Fotodiode wurden in Echtzeit im Messfenster der PhyPiDAQ-Software dargestellt. Die Messdaten wurden in .csv-Datei gespeichert um bestimmte Eigenschaften, wie der Maximum Power Point (MPP) und der Füllfaktor der Fotodiode daraus zu errechnen.
|
 |
Numerische Lösung der Differentialgleichung eines Fadenpendels (ohne und mit Dämpfung). Die Masse und die Länge des Pendels sowie den Dämpfungsfaktor können Sie durch Sliders einstellen.
|
 |
Numerische Lösung der Differentialgleichung eines Federpendels (ohne und mit Dämpfung). Die Masse und die Federkonstante des Pendels sowie den Dämpfungsfaktor können Sie durch Sliders einstellen.
|
 |
Numerische Lösung der Differentialgleichung eines gedämpften Federpendels, welches durch eine sinusförmige Kraft angeregt wird. Die Masse und die Federkonstante des Pendels sowie den Dämpfungsfaktor können Sie durch Sliders einstellen. Die Wirkung der Kreisfrequenz der äußeren Kraft auf die Elongation des Pendels kann man durch die Betätigung des entsprechenden Sliders untersuchen. Die Eigenfrequenz des realen Pendels wird errechnet und ausgegeben. Diese kann man mit der Frequenz der äußeren Funktion vergleichen.
|
 |
Numerische Lösung der Differentialgleichung zum Newtonschen Abkühlungsgesetzes. Die Anfangstemperatur des Körpers T0, die Umgebungstemperatur und die Abkühlungskonstante k können Sie durch Sliders einstellen.
|